Finding Percentiles with the Normal Distribution

A percentile is the value in a normal distribution that has a specified percentage of observations beneath it. Percentiles are often used in standardized tests similar the GRE and in comparing peak and weight of children to gauge their development relative to their peers. The table below shows a portion of the percentile ranks for verbal and quantitative scores on the GRE exam. For case, if you scored 166 on the quantitative reasoning portion of the GRE, then 91% of those who took the test scored lower than y'all. If your score was 153, then 51% of those taking the exam scored lower than you lot.

Scaled

Score

Quantitative Reasoning

Percentile Rank

170

97

169

97

168

95

167

93

166

91

165

89

164

87

163

85

162

82

161

79

160

76

159

73

158

seventy

157

67

156

63

155

59

154

55

153

51

We might ask, "In a population of 60 yr old men with a hateful BMI = 29 and due south=half dozen, what is the xcthursday percentile for BMI?"

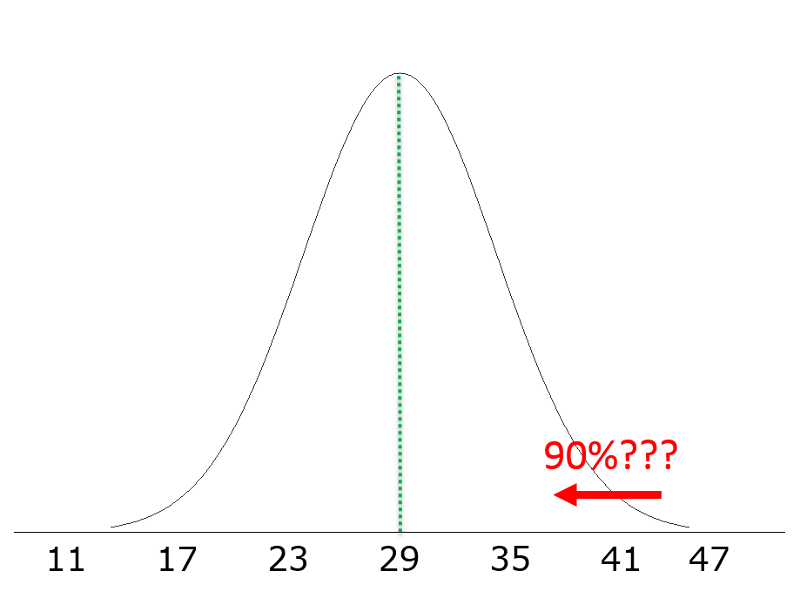
Previously, we started with a value, and asked what was the probability of values less (or greater) than that. However, we are now asking a problem that runs in the other direction. Nosotros are given the proportion or probability (90th percentile) and asked what value of BMI that corresponds to.

Consequently, we use the previous concept and equation, only we work backwards.

First, we go the Z table and find the probability closest to 0.ninety and decide what the corresponding Z score is.

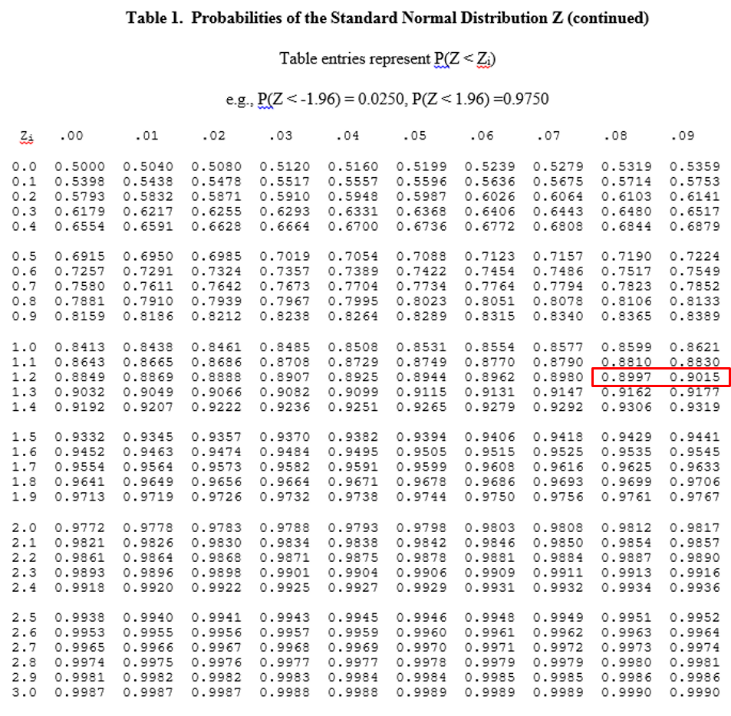
For any normal distribution a probability of 90% corresponds to a Z score of most 1.28.

We besides could have computed this using R by using the qnorm() office to find the Z score respective to a ninety percent probability.

> qnorm(0.ninety)
[ane] 1.281552

So, given a normal distribution with μ =29 and σ =6, what value of BMI corresponds to a Z score of 1.28?

We know that Z=(ten-μ)/σ.

Previously, we knew x, μ, and σ and computed Z. Now, we know Z, μ, and σ, and nosotros demand to compute X, the value respective to the ninetyth percentile for this distribution. Nosotros tin do this by rearranging the equation to solve for "x".

 x = μ + Z σ

In this example, x = 29 + 1.28(vi) = 36.7

Determination: 90% of 60 year old men take BMI values less than 36.7.

Test Yourself

The height of 12 month onetime boys is usually distributed with μ=76.4, σ=2.9 cm. What is the 10th percentile for peak?

Reply

return to elevation | previous page | next page